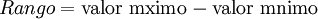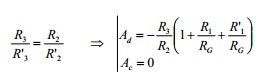La especificación de un instrumento de medición, es una detallada descripción de las
características que identifican al instrumento.
La utilidad y simplicidad de las especificaciones debe tenerse en cuenta al diseñar la
presentación de estas especificaciones. Una especificación que se aplica a todos los rangos, a
todos los niveles y a un amplio rango de condiciones ambientales es fácilmente entendida.
Los componentes que integran la especificación de un instrumento de medición, incluye todos
los parámetros que identifican al instrumento, y a las condiciones de respuesta del mismo ante
diversas condiciones ambientales y de lectura. Entre ellas tenemos los Rangos, la Exactitud, la
Precisión, la Resolución, linealidad, los límites de temperatura de funcionamiento y
almacenamiento, las características de entrada, los valores máximos y mínimo de lectura.
RANGO: Los rangos son las distintas escalas que el instrumento tiene a fin de dar una lectura
adecuada dentro de la resolución establecida en la especificación.
Fondo (FULL)de escala: Es el máximo valor de lectura en la escala en uso.
Factor de escala: Este esta dado por la relación entre el rango elegido y el número de
divisiones de dicho rango. Este es más aplicable a instrumentos de medición analógica.
Factor de escala = RANGO
N° de divisiones
absoluto. O sea, es la exactitud de la medición. En multímetros digitales, la precisión se
expresa por dos términos. Uno de ellos es la cantidad de dígitos fijos de error y el otro termino
puede expresarse de cuatro formas:
Error % = (100)* (valor indicado) - (Valor Verdadero)
Valor Verdadero
las lecturas dentro de la especificaciones indicadas. En consecuencia, periódicamente debe
hacerse una constatación del instrumento con otro de mayor estabilidad y precisión a fin de
ajustarlo mediante los controles adecuados a los valores indicados por la especificación.
LINEALIDAD: Es la máxima desviación de la lectura del instrumento con respecto a una línea recta que une los puntos extremos del rango de medición. Cuanto mas lineal sea el instrumento mas preciso será.
SENSIBILIDAD: Es la habilidad de un instrumento para indicar pequeños cambios de la magnitud medida. Así por ejemplo un multímetro digital de 5 dígitos con un rango de 100 mV de fondo de escala, tiene una sensibilidad de 1 µV. O sea que la menor lectura de voltaje que puede hacer es de 1µV. Este concepto se aplica mas en instrumentos analógicos.
RESOLUCION: Es el menor valor de lectura que puede identificar el instrumento en la escala
en uso. O sea, es el menor cambio de la magnitud que puede ser indicado por el instrumento.
Por ejemplo, en un multímetro de 5 dígitos puede mostrar 200000 cuentas, y en consecuencia
la resolución será igual a 1 dígito. Por ejemplo, 1 Microvoltios en la escala de 200 V.
IMPEDANCIA DE ENTRADA: Al intentar medir una magnitud, el instrumento necesita
afectar el valor de esa magnitud medida a fin de cuantificarla. La impedancia de entrada es
una medida de la capacidad del instrumento de medir esa magnitud, afectándola el menor
grado posible. En consecuencia, a mayor impedancia de entrada, mejor será la calidad del
instrumento de medida.
En los instrumentos analógicos esta es variable de acuerdo al rango utilizado y se expresa en
OHM/volts Resp (Resistencia específica). La resistencia de entrada es:
Rv = Resp (Kohm/V) x Rango (v)
En los instrumentos digitales, la resistencia de entrada es un valor fijo que depende del modo
de lectura (Voltios o Amperes) independiente de la escala usada. En modo de medición de
Tensión la impedancia se mide en Megohms.
En el caso de medición de corriente, se dá también la máxima caída de tensión que se produce
en los terminales de entrada del instrumento.
CONDICIONES AMBIENTALES DE USO: Son las condiciones ambientales (temperatura y
humedad, polvo) y posición en las cuales pueden ser usados los instrumentos, y en las cuales
se cumplen las especificaciones indicadas por los manuales.
Dependiendo del instrumento, se indican las temperaturas máximas y mínimas dentro de las
cuales pueden ser usados, y las temperaturas máximas y mínimas dentro de las cuales pueden
ser guardados. Normalmente el rango de temperaturas de almacenamiento es mayor al de
operación.
En cuanto a la humedad, se aplica los mismos conceptos que para la temperatura, siendo
expresado los límites en % de humedad ambiente.
En los instrumentos digitales normalmente no se aplica este concepto, debido a que la
cuantificación de la información medida se hace por medios electrónicos, no haciéndose uso
de elementos mecánicos, por lo cual la posición no afecta a la lectura.
En los instrumentos de bobina móvil, ya que la indicación de la lectura se hace a través de
aguja acoplada a una bobina móvil que se desplaza radialmente en un campo magnético
generado por un cilindro magnético, se debe indicar la posición en que se debe colocar el
instrumento. Normalmente se indica con un símbolo, para indicar que se debe usar en
posición horizontal con el visor hacia arriba. Esto es debido a que en esta posición, el peso de
la aguja no afecta a la medición realizada.
Un ejemplo de un Formato de Especificaciones es el de la figura 7.2 que trata sobre un Multimetro digital,
en este formato hablan sobre dos modelos, el HP 3466A y el HP 3400A como podemos observar en la figura 7.1.
 |
| Figura 7.2 |
En este formato podemos observar en la parte de especificaciones unas tablas (tablas de especificaciones), las cuales nos dan a conocer los rangos, la precisión entre otras características dependiendo de la tabla que estemos observando, en la figura 7.3 tenemos la tabla de especificación de voltaje en D.C, en ella nos muestran la precisión y la forma de muestreo de los displays dependiendo del rango que vallamos a manejar.
 |
| Figura 7.3 |
Recomendación importante es la de manejar siempre en el rango mayor pero mas cercano de nuestra medida para así poder obtener la mejor resolución de nuestra medición.


 , la media aritmética se define como:
, la media aritmética se define como: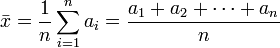
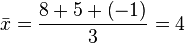
 ), mientras que la letra µ (mu) se usa para la media aritmética de una población, es decir, el valor esperado de una variable.
), mientras que la letra µ (mu) se usa para la media aritmética de una población, es decir, el valor esperado de una variable.![\sqrt[n]{x_1 x_2 \dots x_n} \le \frac{x_1+ \dots + x_n}{n}](http://upload.wikimedia.org/math/8/e/6/8e601c29ce3964e378346560bff6a281.png)

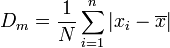
 , la desviación absoluta respecto a la mediana,
, la desviación absoluta respecto a la mediana,  , y la desviación típica,
, y la desviación típica,  , de un mismo conjunto de valores cumplen la desigualdad:
, de un mismo conjunto de valores cumplen la desigualdad: