"La Estadística estudia métodos científicos para recoger, organizar, resumir y analizar datos, así como para sacar conclusiones validas y tomar decisiones razonables basadas en tal análisis"
Murray R. Spiegel.
6.1. Media aritmética
En matemáticas y estadística, la media aritmética (también llamada promedio o simplemente media) de un conjunto finito de números es el valor característico de una serie de datos cuantitativos objeto de estudio que parte del principio de la esperanza matemática o valor esperado, se obtiene a partir de la suma de todos sus valores dividida entre el número de sumandos. Cuando el conjunto es una muestra aleatoria recibe el nombre de media muestral siendo uno de los principales estadísticos muestrales.
Expresada de forma más intuitiva, podemos decir que la media (aritmética) es la cantidad total de la variable distribuida a partes iguales entre cada observación.
Por ejemplo, si en una habitación hay tres personas, la media de dinero que tienen en sus bolsillos sería el resultado de tomar todo el dinero de los tres y dividirlo a partes iguales entre cada uno de ellos. Es decir, la media es una forma de resumir la información de una distribución (dinero en el bolsillo) suponiendo que cada observación (persona) tuviera la misma cantidad de la variable.
También la media aritmética puede ser denominada como centro de gravedad de una distribución, el cual no está necesariamente en la mitad.
Una de las limitaciones de la media aritmética es que se trata de una medida muy sensible a los valores extremos; valores muy grandes tienden a aumentarla mientras que valores muy pequeños tienden a reducirla, lo que implica que puede dejar de ser representativa de la población.
6.1.1. Definición.
Dados los n números 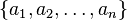 , la media aritmética se define como:
, la media aritmética se define como:
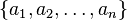 , la media aritmética se define como:
, la media aritmética se define como: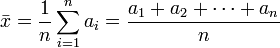
Por ejemplo, la media aritmética de 8, 5 y -1 es igual a:
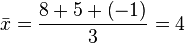
Se utiliza la letra X con una barra horizontal sobre el símbolo para representar la media de una muestra ( ), mientras que la letra µ (mu) se usa para la media aritmética de una población, es decir, el valor esperado de una variable.
), mientras que la letra µ (mu) se usa para la media aritmética de una población, es decir, el valor esperado de una variable.
 ), mientras que la letra µ (mu) se usa para la media aritmética de una población, es decir, el valor esperado de una variable.
), mientras que la letra µ (mu) se usa para la media aritmética de una población, es decir, el valor esperado de una variable.
En otras palabras, es la suma de n valores de la variable y luego dividido por n : donde n es el número de sumandos, o en el caso de estadística el número de datos.
6.1.2. Propiedades
- La suma de las desviaciones con respecto a la media aritmética es cero (0).
- La media aritmética de los cuadrados de las desviaciones de los valores de la variable con respecto a una constante cualquiera se hace mínima cuando dicha constante coincide con la media aritmética.
- Si a todos los valores de la variable se le suma una misma cantidad, la media aritmética queda aumentada en dicha cantidad.
- Si todos los valores de la variable se multiplican por una misma constante la media aritmética queda multiplicada por dicha constante.
- La media aritmética de un conjunto de números positivos siempre es igual o superior a la media geométrica:
- La media aritmética está comprendida entre el valor máximo y el valor mínimo del conjunto de datos:
6.2. Desviación de la media.
Es la diferencia en valor absoluto entre cada valor de la variable estadística y la media aritmética.
Di = |x - x|
6.3. Desviación media.
En estadística la desviación absoluta promedio o, sencillamente desviación media o promedio de un conjunto de datos es la media de las desviaciones absolutas y es un resumen de la dispersión estadística. Se expresa, de acuerdo a esta fórmula:
La desviación absoluta respecto a la media,  , la desviación absoluta respecto a la mediana,
, la desviación absoluta respecto a la mediana,  , y la desviación típica,
, y la desviación típica,  , de un mismo conjunto de valores cumplen la desigualdad:
, de un mismo conjunto de valores cumplen la desigualdad:
 , la desviación absoluta respecto a la mediana,
, la desviación absoluta respecto a la mediana,  , y la desviación típica,
, y la desviación típica,  , de un mismo conjunto de valores cumplen la desigualdad:
, de un mismo conjunto de valores cumplen la desigualdad:
Siempre ocurre que
donde el Rango es igual a:
El valor:

ocurre cuando los datos son exactamente iguales e iguales a la media aritmética y

cuando solo hay dos valores en el conjunto de datos.
6.4. Desviacion Estandar.
La desviación estándar o desviación típica (denotada con el símbolo σ o s, dependiendo de la procedencia del conjunto de datos) es una medida de centralización o dispersión para variables de razón (ratio o cociente) y de intervalo, de gran utilidad en la estadística descriptiva.
Se define como la raíz cuadrada de la varianza. Junto con este valor, la desviación típica es una medida (cuadrática) que informa de la media de distancias que tienen los datos respecto de su media aritmética, expresada en las mismas unidades que la variable.
Para conocer con detalle un conjunto de datos, no basta con conocer las medidas de tendencia central, sino que necesitamos conocer también la desviación que presentan los datos en su distribución respecto de la media aritmética de dicha distribución, con objeto de tener una visión de los mismos más acorde con la realidad al momento de describirlos e interpretarlos para la toma de decisiones.
La desviación estándar es una medida del grado de dispersión de los datos con respecto al valor promedio. Dicho de otra manera, la desviación estándar es simplemente el "promedio" o variación esperada con respecto a la media aritmética.
Por ejemplo, las tres muestras (0, 0, 14, 14), (0, 6, 8, 14) y (6, 6, 8, 8) cada una tiene una media de 7. Sus desviaciones estándar muestrales son 7, 5 y 1 respectivamente. La tercera muestra tiene una desviación mucho menor que las otras dos porque sus valores están más cerca de 7.
La desviación estándar puede ser interpretada como una medida de incertidumbre. La desviación estándar de un grupo repetido de medidas nos da la precisión de éstas. Cuando se va a determinar si un grupo de medidas está de acuerdo con el modelo teórico, la desviación estándar de esas medidas es de vital importancia: si la media de las medidas está demasiado alejada de la predicción (con la distancia medida en desviaciones estándar), entonces consideramos que las medidas contradicen la teoría. Esto es coherente, ya que las mediciones caen fuera del rango de valores en el cual sería razonable esperar que ocurrieran si el modelo teórico fuera correcto. La desviación estándar es uno de tres parámetros de ubicación central; muestra la agrupación de los datos alrededor de un valor central (la media o promedio).
6.4.1Distribución de probabilidad continua
Es posible calcular la desviación estándar de una variable aleatoria continua como la raíz cuadrada de la integral
donde
6.4.2Distribución de probabilidad discreta
La DS es la raíz cuadrada de la varianza de la distribución de probabilidad discreta
Así la varianza es la media de los cuadrados de las diferencias entre cada valor de la variable y la media aritmética de la distribución.
Aunque esta fórmula es correcta, en la práctica interesa realizar inferencias poblacionales, por lo que en el denominador en vez de n, se usa n-1 (Corrección de Bessel) Esta ocurre cuando la media de muestra se utiliza para centrar los datos, en lugar de la media de la población. Puesto que la media de la muestra es una combinación lineal de los datos, el residual a la muestra media se extiende más allá del número de grados de libertad por el número de ecuaciones de restricción - en este caso una. Dado esto a la muestra así obtenida de una muestra sin el total de la población se le aplica esta corrección con la fórmula desviación estándar muestral. Cuando los casos tomados son iguales al total de la población se aplica la fórmula de desviación estándar poblacional.
También hay otra función más sencilla de realizar y con menos riesgo de tener equivocaciones :
![\sqrt[n]{x_1 x_2 \dots x_n} \le \frac{x_1+ \dots + x_n}{n}](http://upload.wikimedia.org/math/8/e/6/8e601c29ce3964e378346560bff6a281.png)

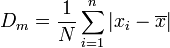


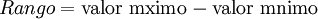





No hay comentarios:
Publicar un comentario